American Approximation: Barone-Adesi and Whaley [Loxx]

4 Eki 2022

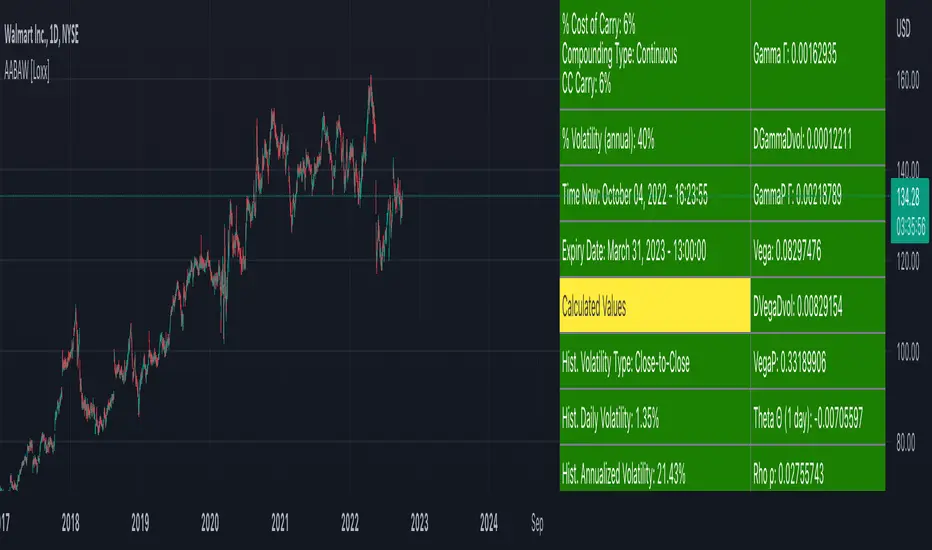
American Approximation: Barone-Adesi and Whaley [Loxx] is an American Options pricing model. This indicator also includes numerical greeks. You can compare the output of the American Approximation to the Black-Scholes-Merton value on the output of the options panel.

An American option can be exercised at any time up to its expiration date. This added freedom complicates the valuation of American options relative to their European counterparts. With a few exceptions, it is not possible to find an exact formula for the value of American options. Several researchers have, however, come up with excellent closed-form approximations. These approximations have become especially popular because they execute quickly on computers compared to numerical techniques. At the end of the chapter, we look at closed-form solutions for perpetual American options.

The Barone-Adesi and Whaley Approximation
The quadratic approximation method by Barone-Adesi and Whaley (1987) can be used to price American call and put options on an underlying asset with cost-of-carry rate b. When b > r, the American call value is equal to the European call value and can then be found by using the generalized Black-Scholes-Merton (BSM) formula. The model is fast and accurate for most practical input values.

American Call
C(S, C, T) = Cbsm(S, X, T) + A2 / (S/S*)^q2 ... when S < S*

C(S, C, T) = S - X ... when S >= S*

where Cbsm(S, X, T) is the general Black-Scholes-Merton call formula, and

A2 = S* / q2 * (1 - e^((b - r) * T)) * N(d1(S*)))

d1(S) = (log(S/X) + (b + v^2/2) * T) / (v * T^0.5)

q2 = (-(N-1) + ((N-1)^2 + 4M/K))^0.5) / 2

M = 2r/v^2

N = 2b/v^2

K = 1 - e^(-r*T)

American Put
P(S, C, T) = Pbsm(S, X, T) + A1 / (S/S**)^q1 ... when S < S**

P(S, C, T) = X - S .... when S >= S**

where Pbsm(S, X, T) is the generalized BSM put option formula, and

A1 = -S** / q1 * (1 - e^((b - r) * T)) * N(-d1(S**)))

q1 = (-(N-1) - ((N-1)^2 + 4M/K))^0.5) / 2

where S* is the critical commodity price for the call option that satisfies

S* - X = c(S*, X, T) + (1 - e^((b - r) * T) * N(d1(S*))) * S* * 1/q2

These equations can be solved by using a Newton-Raphson algorithm. The iterative procedure should continue until the relative absolute error falls within an acceptable tolerance level. See code for details on the Newton-Raphson algorithm.

Inputs
S = Stock price.
K = Strike price of option.
T = Time to expiration in years.
r = Risk-free rate
c = Cost of Carry
V = Variance of the underlying asset price
cnd1(x) = Cumulative Normal Distribution
cbnd3(x) = Cumulative Bivariate Normal Distribution
nd(x) = Standard Normal Density Function
convertingToCCRate(r, cmp) = Rate compounder

Numerical Greeks or Greeks by Finite Difference
Analytical Greeks are the standard approach to estimating Delta, Gamma etc... That is what we typically use when we can derive from closed form solutions. Normally, these are well-defined and available in text books. Previously, we relied on closed form solutions for the call or put formulae differentiated with respect to the Black Scholes parameters. When Greeks formulae are difficult to develop or tease out, we can alternatively employ numerical Greeks - sometimes referred to finite difference approximations. A key advantage of numerical Greeks relates to their estimation independent of deriving mathematical Greeks. This could be important when we examine American options where there may not technically exist an exact closed form solution that is straightforward to work with. (via VinegarHill FinanceLabs)

Things to know

• Only works on the daily timeframe and for the current source price.
  
• You can adjust the text size to fit the screen
  

4 Eki 2022

Sürüm Notları

Corrected string constant error.

4 Eki 2022

Sürüm Notları

Readded compounding.

28 Şub

Sürüm Notları

fixed error